Multitone-harmonic-balance-method-example
Example application of multitone harmonic balance method on Duffing Van Der Pol equation
An example about the application of multitone harmonic balance method to Duffing Van Der Pol equation
Example:
Test System

Test parameters
mu=0.5; c11=10^2; c13=5; c13d=0.15;
c=1;
au0=8c;
au1=10c;
au2=15*c;
%TEST 1——————————————————–
% input frequency
w1 = 1.3;%rad/s
w2 = 2.7;%rad/s
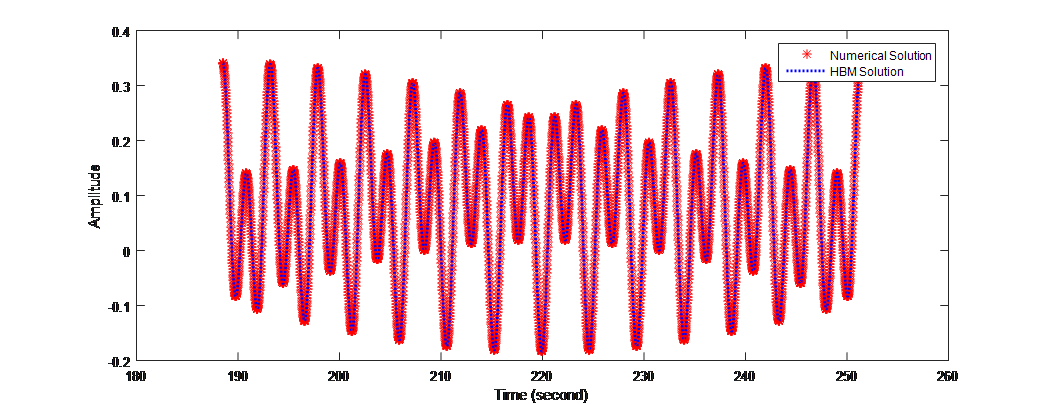
%TEST 2——————————————————-
%change frequency
% input frequency
w1 = 10;%rad/s
w2 = 1;%rad/s
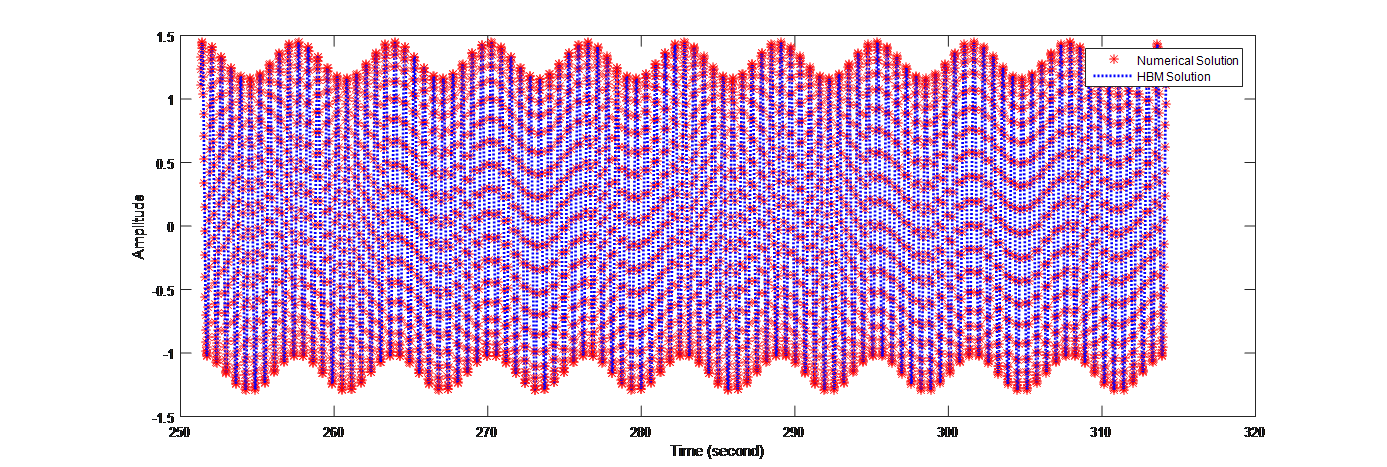
%TEST 3——————————————————-
c=5; % change amplitude
au0=8c;
au1=10c;
au2=15*c;
% input frequency
w1 = 10;%rad/s
w2 = 1;%rad/s
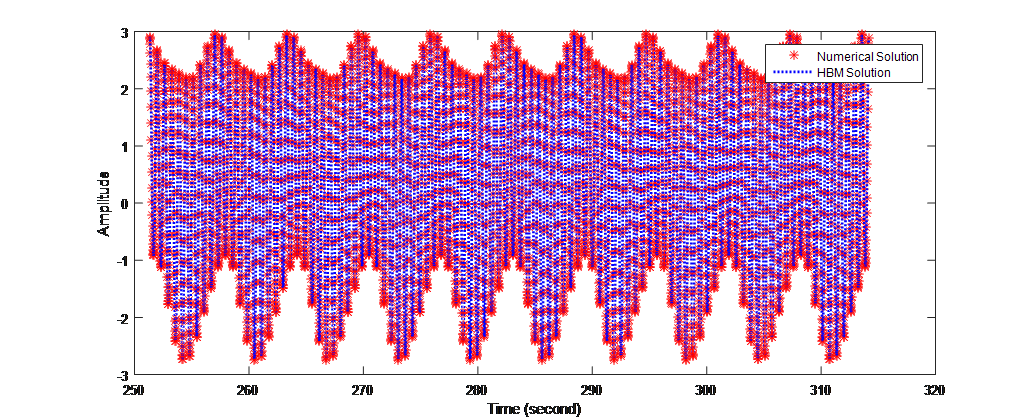
%TEST 4——————————————————-
Command window output
c=5;
au0=8c;
au1=10c;
au2=15*c;
% input frequency
w1 = 3.2;%rad/s
w2 = 1.8;%rad/s
compute hbe solution:
costhbe =
2.9173e-26
compute numerical solution:
mse_err =
47.3915
mse_err =
9.0363
mse_err =
1.0226e-07
mse_err =
7.0438e-12
Amplitudes of components:
constant :0.37613
0w1+1w2 :0.73122
0w1+2w2 :0.014166
1w1-2w2 :0.0083522
1w1-1w2 :0.018504
1w1+0w2 :0.51892
1w1+1w2 :0.023698
1w1+2w2 :0.014597
2w1-2w2 :0.001303
2w1-1w2 :0.0069842
2w1+0w2 :0.0088012
2w1+1w2 :0.015925
2w1+2w2 :0.019746
Reference studies:
https://link.springer.com/article/10.1007/s11071-008-9390-y
https://link.springer.com/article/10.1007/s11071-010-9688-4